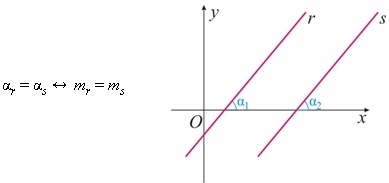
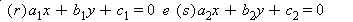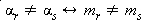A Trigonometria é uma área da Matemática responsável pela relação entre os lados e os ângulos de um triângulo. Nos triângulos retângulos, as relações estabelecem os chamados ângulos notáveis, 30º, 45º e 60º que possuem valores fixos representados para as relações seno, cosseno e tangente. Nos demais triângulos, as condições são adaptadas na busca pela relação existente entre os ângulos e os lados.
Alguns estudos dizem que Antes de Cristo um grego chamado Hiparco colocou em prática as relações dos ângulos de um triângulo retângulo e acredita-se também que a primeira tabela trigonométrica foi feita por ele. Assim, dentro da matemática ele é conhecido e respeitado como o “Pai da Trigonometria”.
Devemos ressaltar que a Trigonometria objetivou a elaboração dos estudos das funções trigonométricas, relacionadas aos ângulos e aos fenômenos periódicos. A partir do século XV, a modernidade dos cálculos criou novas situações teóricas e práticas relacionadas aos estudos dos ângulos e das medidas. Com a criação do Cálculo Diferencial e Integral, pelos cientistas Isaac Newton e Leibniz, a Trigonometria ganhou moldes definitivos no cenário da Matemática, sendo constantemente empregada em outras ciências, como Medicina, Engenharia, Física (ondulatória, óptica), Química, Geografia, Astronomia, Biologia, Arquitetura, Cartografia, Navegação entre outras.
Aplicação da trigonometria
Muitos fenômenos físicos e sociais de comportamento cíclico, ou periódico, podem ser modelados por funções trigonométricas. Daí a enorme aplicação desse estudo em campos variados da ciência, como Acústica, Astronomia, Economia ou Medicina. Uma circunstância exemplar é o monitoramento da frequência cardíaca, isto é, do número de batimentos cardíacos em um período de tempo, geralmente medido em bpm (batimentos cardíacos por minutos). Apresente a eles uma situação para eles possam refletir sobre o assunto, como exemplo:
No gráfico abaixo, a variação da pressão sanguínea P (em mmHg) de certo indivíduo, em função do tempo, em segundos, é uma função cíclica, sendo que cada ciclo completo (período) equivale a um batimento cardíaco.
Trigonometria com molas