FUNÇÃO MODULAR
A função modular tem várias aplicações no cotidiano, como por exemplo a aplicação em comparação das temperaturas entre duas ou mais cidade, na Física, na Química na Geografia entre outras. Para entender função modular - tema que cai nos vestibulares e no Enem - devemos compreender o que é módulo. Em seguida, através de exercícios, resolveremos algumas equações modulares e falaremos sobre a função modular:
MóduloAntes de falar da função modular, vamos relembrar a definição e como calcular o módulo de um número. O módulo é a distância de um determinado número até o zero. Por exemplo, o módulo de 13 é a distância entre o 13 e o 0. Para nos deslocarmos do 13 ao 0, andaremos 13 unidades. Portanto, o módulo de 13 é igual a 13. Ou ainda: |13| = 13. Sendo assim, qual será o módulo de -13? Bem, a distância do -13 ao zero é também de 13 unidades. Então, |-13| = 13.
Módulo de um número real
O módulo ou valor absoluto de um número real x é representado por |x|, que lemos: módulo de x.
1º - Se x for um número real positivo o módulo de x será o próprio x.2º - Se x for um número real negativo o módulo de x será o x positivo.
Resumindo | - x | = x | x | = x
Obs: O módulo pode ser interpretado como a distância, na reta real, de um número real x a origem (zero)
Considere a reta real:

Chamamos a distância de um ponto da reta à origem (distância do ponto até o zero) de módulo ou valor absoluto.
Assim, a distância do ponto 4 à origem é 4. Dizemos que o módulo de 4 é igual a 4. E representamos por |4| = 4
Da mesma forma, a distância do ponto -2 à origem é 2, ou seja, o módulo de -2 é 2, pois não há sentido em considerarmos distâncias negativas. Assim: |-2| = 2
https://www.youtube.com/watch?v=IxdTj9j_Fig
EXERCÍCIO SOBRE FUNÇÃO







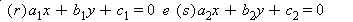
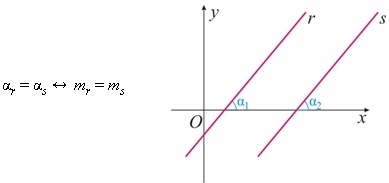
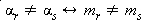


















.jpg)
.jpg)
.jpg)
.jpg)

.jpg)
